Jointly published by The Division of General Studies, Chukwuemeka Odumegwu Ojukwu University, Nigeria (formerly Anambra State University) and Klamidas.com Global Online Journal of Academic Research (GOJAR), Vol. 4, No. 1, February 2025. https://klamidas.com/gojar-v4n1-2025-02/ |
||||||||||||||
|
Implementation and Comparative Analysis of AMGT Method in Maple 24: Convergence Performance in Optimization Problems Mark Laisin & Rosemary U. Adigwe
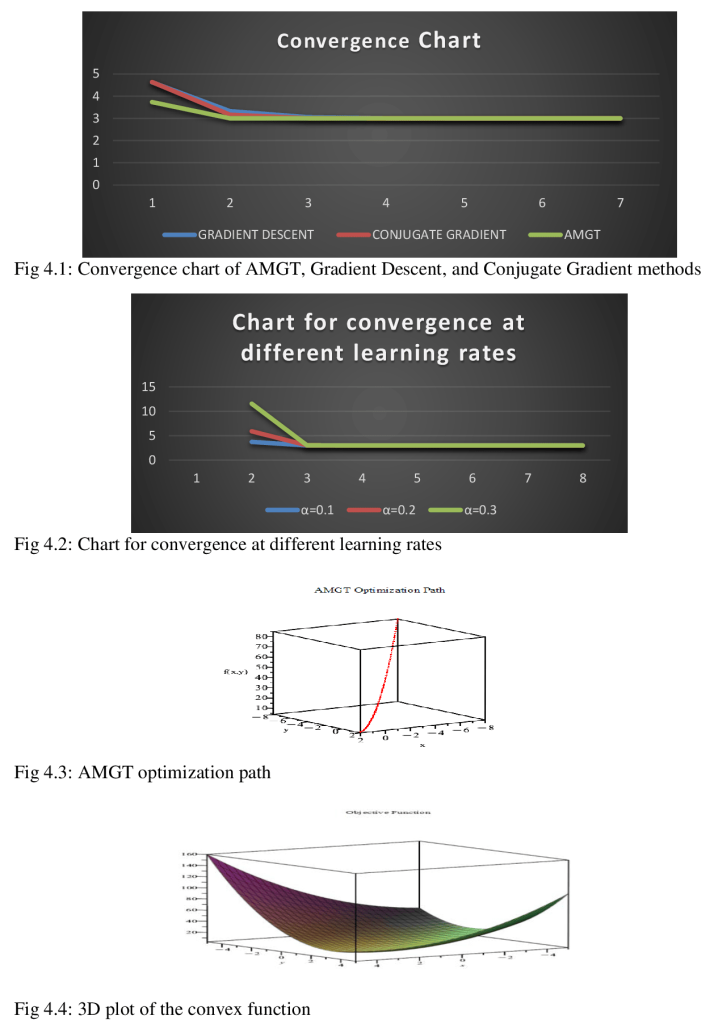
Abstract This study investigates the utilization of the Accelerated Modified Gradient Technique (AMGT) in Maple 24 for optimization problem-solving. The research focuses on enhancing and evaluating the convergence speed of AMGT in comparison to the Gradient Descent (GD) and Conjugate Gradient (CG) methods. The analysis covers a range of function types, such as convex functions (e.g., production cost, energy consumption, and transportation cost functions) and a non-convex function. Findings showcase the effectiveness and versatility of AMGT, shedding light on its utility for addressing practical optimization challenges. Keywords: AMGT method, Maple 24, convergence performance, optimization problems, comparative analysis I. Introduction Optimization techniques are crucial for solving complex problems in various fields, such as engineering, economics, machine learning, and operations research. They are essential for decision-making processes, from designing efficient systems to finding optimal financial strategies (Boyd & Vandenberghe, 2004). Gradient-based methods like Gradient Descent (GD) and Conjugate Gradient (CG) are widely used due to their computational efficiency and well-understood theoretical properties (Nocedal & Wright, 2006). These methods iteratively improve solutions by using gradients to guide the search for the optimal solution, making them effective for continuous optimization problems. However, in some cases, basic gradient-based methods face limitations in terms of convergence speed and stability, especially in large or complex problem spaces. As optimization problems become high-dimensional or non-convex, traditional methods like GD and CG may struggle, leading to slower convergence rates and potential failure to escape local minima (Bertsekas, 1999). Accelerated Gradient Methods, including the Accelerated Modified Gradient Technique (AMGT), have been proposed to address these challenges and offer improvements in convergence speed and stability (Nesterov, 1983). The AMGT combines the theoretical robustness of traditional gradient methods with acceleration strategies that optimize the search for a minimum. It adapts the gradient direction dynamically to enhance the rate of convergence, a feature that can be critical when dealing with large-scale optimization tasks or when high precision is required (Dauphin et al., 2015). Despite its potential, there is a limited comparative analysis of AMGT concerning traditional methods such as GD and CG in contemporary optimization applications, particularly in symbolic and numerical computation environments. This paper investigates the implementation of AMGT in Maple 24, a versatile software for mathematical modeling, simulation, and optimization (Maplesoft, 2023). The objective is to compare the convergence performance of AMGT with GD and CG across various optimization problems, including convex and non-convex scenarios, to assess their relative effectiveness in different contexts.
References Bertsekas, D. P. (1999). Nonlinear Programming (2nd ed.). Athena Scientific. Boyd, S., & Vandenberghe, L. (2004). Convex Optimization. Cambridge University Press. Dauphin, Y. N., Pascanu, R., Gulcehre, C., Cho, K., Ganguli, S., & Bengio, Y. (2015). Identifying and attacking the saddle point problem in high-dimensional non-convex optimization. In Proceedings of the 34th International Conference on Machine Learning (Vol. 37, pp. 2967-2975). Diederikm, P. K and Jimmy, L. B. (2015). Adam: A method for Stochastic Optimization. Published as a conference paper at ICLR, 2015. Kingma, D. P., & Ba, J. (2015). “Adam: A Method for Stochastic Optimization.” arXiv preprint arXiv:1412.6980. MapleSoft. (2023). Maple 24 Documentation. [Online]. Available: https://www.maplesoft.com/documentation. Nesterov, Y. (1983). A method of solving a convex programming problem with convergence rate O(1/k^2). DokladyAkademiiNauk SSSR, 269(3), 543–547. Nesterov, Y. (2004). Introductory Lectures on Convex Optimization: A Basic Course. Springer. Nocedal, J., & Wright, S. J. (2006). Numerical Optimization (2nd ed.). Springer. Noel J. (2023). Nesterovs Method for Convex Optimization. Society for Industrial and Applied Mathematics. Vol. 65, No. 2, pp. 539–562. Polyak, B. T. (1964). “Some Methods of Speeding up the Convergence of Iteration Methods.” USSR Computational Mathematics and Mathematical Physics, 4(5), 1-17. Rahul, A. (2023). Complete Guide to the Adam Optimization Algorithm. https://builtin.com/machine-learning/adam-optimization. (Retrieved November 11, 2024) Satyam, T (2024)/Adagrad Optimizer Explained: How It Works, Implementation, & Comparisons | DataCamp www.gabormelli.com/RKB/Root_Mean_Square_Propagation_Algorithm_(RMSprop) (Retrieved November 11, 2024).
|
||||||||||||||